Groups Lecture 12

Posted by

5

in which we find out more about quotients, including the quotient map, and prove the Isomorphism Theorem.

We are continuing our investigation of quotients. Today we saw that the group operation on cosets only works when we have a normal subgroup, by looking at the example of a reflection in D_6. We met the very important quotient map q\colon {G\to G/K} which exists for any normal subgroup K\trianglelefteq G. This helped us to see that (subgroups and) quotients of cyclic groups are always cyclic. We then stated the Isomorphism Theorem: if f\colon {G\to H} is a group hom with kernel K, then K\trianglelefteq G (as seen before) and G/K\cong \mathrm{Im}f. We proved this by defining a homomorphism G/K\to H that sends any coset to the image (under f) of any of its elements. Again, as usually with cosets, the main thing is to check that this is well-defined. And once we saw that, we could prove that it is indeed injective, giving us an isomorphism to the image of f as required. As a consequence, when we have an injection f\colon {G\to H} (i.e. the kernel is just the identity element), we can view G as (isomorphic to) a subgroup of H. And if f is a surjection, then the codomain H itself is a quotient of G. A possible slogan for the Isomorphism Theorem could be “homomorphic images are quotients“. As examples we looked at the determinant of an n\times n matrix, we found the unit circle as the quotient \mathbb{R}/\mathbb{Z}, and had a quick look at how many “quadratic residues” there are modulo a prime p.

Understanding today’s lecture

When dealing with quotients, remember that they are not subgroups! The elements are different; if G has elements a\in G, then a quotient G/K has cosets aK as elements, which are themselves subsets of G. You can often calculate with them fairly easily through a representative, because after all the operation is defined as aK*bK=(ab)K, but you have to remember that every coset has several representatives you could have chosen. And it is always good to keep this example in mind: all non-trivial subgroups of \mathbb{Z} are infinite (they are n\mathbb{Z}), and all proper quotients of \mathbb{Z} are finite (they are \mathbb{Z}/n\mathbb{Z}=\mathbb{Z}_n). (The trivial ones here are 0\mathbb{Z}=\{0\} and \mathbb{Z}/0\mathbb{Z}\cong \mathbb{Z}.)

The Isomorphism Theorem is one that we will use over and over again, and eventually we will probably not even notice any more when we are using it. It is that central.

Preparing for Lecture 13

Next time we will look at cyclic groups again, proving that they are essentially unique. That means, up to isomorphism, there is only one cyclic group of any given order. It seems intuitive, but the Isomorphism Theorem and some other results we’ve had will help us prove it very rigorously. So it would be good if you can remind yourself about everything you know about cyclic groups and about subgroups of \mathbb{Z} before next time.

Going a little deeper

The Isomorphism Theorem isn’t really something that is restricted to groups, there is a version of it in many other areas of maths. (And in fact there are other Isomorphism Theorems for groups as well, sometimes called Noether’s Isomorphism Theorems. But our one is “the” (or first) Isomorphism Theorem.) In second year Groups Rings and Modules you’ll see one for rings and one for modules. Either in Vectors and Matrices, or at least in second year Linear Algebra, you will see one for vectorspaces, though it looks different (and a lot easier, because vectorspaces are very nice). The rank-nullity theorem says: if \alpha\colon {V\to W} is a linear map between vectorspaces, then \mathrm{dim}V=\mathrm{rank}(\alpha)+\mathrm{nullity}(\alpha), where the rank is the dimension of the image and the nullity is the dimension of the kernel. If you compare that to our isomorphism theorem and (once you know more about finite dimensional vectorspaces) see what the equivalent would be for vectorspaces, you’ll see it is exactly this.

So, in what sense are quotient groups “the opposite of” kernels? I explained last blog that kernels have a certain universal property. Quotients also have a universal property, but sort of on the other side of the homomorphism. Given f\colon {G\to H} with kernel \iota\colon {K\to G} (viewed as an inclusion), we know that f\iota(k)=e for all k\in K. Writing q\colon {G\to G/K} for the quotient map as in lectures, this q has the same property: q\iota(k)=e for all k\in K. Remember that we can describe this as “the composite q\iota is zero”. Now if we have any other group hom g\colon {H\to L} which also satisfies g\iota(k)=e for all k\in K, then this g factors through the quotient map, in the sense that there is a unique group hom \overline{g}\colon {G/K\to L} satisfying \overline{g}q=g. We saw in the proof of the Isomorphism Theorem one special case of how such a morphism \overline{g} might be defined. Perhaps you can extend that construction to this case? We won’t necessarily get that \overline{g} is injective, like we had in the Isomorphism Theorem, but the rest works just the same.

5 thoughts on “Groups Lecture 12”

  1. Someone asked me after the lecture about the comment “Quotients are not subgroups”. What if we have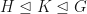 H\trianglelefteq K \trianglelefteq G? Do we then have 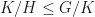K/H \leq G/K? Well, you can work it out: what are the elements of 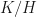K/H? What are the elements of 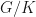G/K? Are they the same type of elements? There is something related in one of the “other” isomorphism theorems (the counting varies from people to people, I think I usually call it the third, or it might be called the fourth by others). If you’re interested, you can find it (dare I say on wikipedia; what I should say is) in any good group theory book.

    Like

    Reply

  2. Since we are using the “same coset check” so much at the moment, I was asked where to find it. It is directly after the proof of Lagrange’s Theorem (Theorem 23), well, after the definition of index. You can also find it if you look at all blogs with the tag “coset”.
    In the second week feedback someone also commented that they would like more structure and numbering in my lecture notes. Well, I do try: I have chapters with numbers, I have sections inside the chapters (feel free to number them), and I have numbers for results (as well as “slogans” or names to remember them by). What might also help is this document. If you find it useful, you can easily make your own for other courses and the rest of groups. It is a very good way of getting an overview over the course (rather than just being stuck in the details of one step to the next).

    Like

    Reply

  3. I feel like I do not much agree on the notation used in the last example of today’s example, where Z/pZ\{0} is used. Z/pZ definitely refers to the quotient group while it still keeps the operation in Z as addition I suppose. But as mentioned, the Zp* has the operation of multiplication. So basically we have (a+pZ)*(b+pZ)=(a+b)+pZ if we are using this notation, which is not correct. I believe what you want to show by using Z/pZ\{0} is all the elements in Zp* but not including the operation. But that probably could mess things up. Looking forward to your reply.

    Like

    Reply

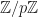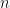    • I can see where your confusion comes from. You are right, we said \mathbb{Z}/p\mathbb{Z} is the group with elements a+p\mathbb{Z} and addition. However, if we take the same elements, which you can write as [a] if you find it easier, and leave out [0], then we get a group under multiplication, which we proved in “mult mod n as a group” (Proposition 29): just put n to be a prime p in that proof/statement. 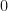When leaving out 0 and not specifying any other group operation, we always mean multiplication as the group operation. If you prefer to write 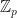\mathbb{Z}_p instead of 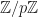\mathbb{Z}/p\mathbb{Z}, that is perfectly fine. 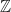But (\mathbb{Z}/p\mathbb{Z})^*= (\mathbb{Z}/p\mathbb{Z})\setminus \{[0]\} is also correct notation. In fact, you will learn in second year some more aspects of this: it is actually a ring, which means it has addition and multiplication on it which interact in a nice way (via the distributive law, if you want to look it up). And of course \mathbb{Z} is such a ring, we can add and multiply there, and both those operations carry over to 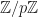\mathbb{Z}/p\mathbb{Z}, as we saw in the section “Applications of Lagrange” when we proved that addition and multiplication 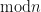\mathrm{mod} n are well-defined.

      Like

      Reply

Leave a comment